Est-ce que l’utilisation des sensibilités dans l’explication du P&L est une méthode efficace de mesure de la rentabilité et d’identification des facteurs de risque de marché?
Last Updated on April 29,2020
1.Qu’est-ce que le P&L?
L’un des objectifs principaux du Front Office d’une banque de marché,subdivisé en lignes de métier spécialisées dites «desks de trading »,est la recherche du compromis optimal entre risque et rentabilité.
Le Profit&Loss Account(compte de perte et de profit)ou P&L en abrégé,permet de mesurer la rentabilité des desks de trading sur une période donnée(rentabilité journalière,mensuelle,annuelle,etc.).
Concrètement,le P&L se compose de quatre principaux termes,le premier est la variation de valeur des positions en « vie »,non échu du desk sur la période,le deuxième est l’ensemble des flux monétaires entrant ou sortant du desk sur la période,le troisième constitue les ajustements de valeurs spécifiques(réserves,ajustements particuliers dus au modèle de valorisation utilisé,ajustement de change,etc.),le quatrième constitue l’ensemble des frais financiers lié au passage d’ordre.
La somme de ces quatre composantes constitue le P&L net de la période d’évaluation:
\[P\&L(t;t+h)=P(t+h;ζ_{t+h})-P(t;ζ_{t})+Add-On(t;t+h)\space \space(i)\]
Avec:
\[Add-On(t;t+h)=\sum_{i=t}^{t+h}CashFlows(i)+\sum_{j=t}^{t+h}Adjustments(j)+\sum_{k=t}^{t+h}Fees(k)\space \space(ii)\]
Il est à noter que \(P(t;ζ_{t})=MtM(desk-trans.,t)\)constitue la valeur de marché de l’ensemble des transactions du desk à la date t.
Le calcul de cette valeur de marché peut être simple si les transactions considérées sont simples et si leur prix peut être facilement observé sur le marché.En revanche dans le cadre de produits plus complexes(produits exotiques,fortement path-dependent,structurés,etc.)la valorisation nécessite l’utilisation de modèles complexes et qui peuvent générer des incertitudes quant à la fiabilité des niveaux de P&L calculés.
2.Utilisation des sensibilités dans l’explication du P&L
a.Principe
Le P&L est utilisé comme décrit plus haut par bon nombre d’institutions financières en tant que mesure de rentabilité économique des activités de marché sur une période donnée.
Entre deux périodes,l’observation d’une variation du niveau de cette mesure conduit à la détermination des facteurs ayant entrainé cette variation et à optimiser la composition du portefeuille en conséquence.
L’idée est d’arriver au compromis optimal entre facteurs d’exposition/de risque et le revenue de l'activité. C’est la gestion du risque.
Une hypothèse souvent effectué est que la fonction \(P(t ;ζ_{t})\) et donc le P&L est une fonction \(C^{n+1}\) sur \(I = R * R^p \) à valeur dans R et donc le théorème de Taylor est applicable.
Concrètement, dans le cadre d’une option, on peut par exemple écrire :
\(P(t ; ζ_{t}) = F(t,S_t,σ_t) , \) avec \(ζ_{t} = \{S_t,σ_t\} \space \space (iii)\)
Variables utilisées :
- \(S_t\) : Cours de l’actif sous-jacent
- \(σ_t\) : Volatilité de l’actif sous-jacent
L’application du théorème de Taylor nous conduit donc à l’expression suivante :
\[ {∆P(t ; ζ_{t})} = { ∆F (t,S_t,σ_t)} \space \space (iv)\]
\[ {∆P(t ; ζ_{t})} = {\partial F (t,S_t,σ_t) \over \partial t} ∆t + {\partial F (t,S_t,σ_t) \over \partial S_t} ∆S_t + {\partial F (t,S_t,σ_t) \over \partial σ_t} ∆σ_t \]
\[ + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial S_t^2} (∆S_t)^2 + {\partial^2 F (t,S_t,σ_t) \over \partial S_t \partial σ_t} ∆S_t ∆σ_t + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial σ_t^2} (∆σ_t)^2 \space \space (v)\]
Cette réécriture de la variation de valeur du portefeuille entre deux instants en termes de dérivées partielles de la fonction de valorisation du prix de marché de portefeuille est appelée l’explication du P&L en fonction des sensibilités de marché de premiers et seconds ordre.
b. Avantages/Inconvénients
Le point fort de cette écriture de la variation de valeur du portefeuille de transactions en fonction de variations données de ses paramètres de réévaluation (i.e. facteurs de risque), est de pouvoir attribuer le niveau du P&L à une variation de la courbe de taux, de la volatilité, de la valeur du sous-jacent, etc.
Le P&L et l’explication du P&L ci-dessus sont donc des éléments centraux du processus de gestion des risques, qui sont mesurés et analysés quotidiennement dans les banques d’investissements.
En effet, il est possible d’immuniser le portefeuille et donc le P&L contre les variations d’un facteur de risque donné (e.g. niveau de volatilité, niveau du sous-jacent, etc.).
Toutefois, il est à rappeler que le développement de Taylor n’est pas une égalité et de fait, il existe un reste dit reste intégral par application du théorème fondamental de l’analyse :
\[ {∆P(t ; ζ_{t})}= Explained Var(P(t ; ζ_{t}))+Unexplained Var(P(t ; ζ_{t})) \space \space (vi)\]
Avec:
\[ Explained Var(P(t ; ζ_{t})) = {\partial F (t,S_t,σ_t) \over \partial t} ∆t + {\partial F (t,S_t,σ_t) \over \partial S_t} ∆S_t + {\partial F (t,S_t,σ_t) \over \partial σ_t} ∆σ_t \]
\[ + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial S_t^2} (∆S_t)^2 + {\partial^2 F (t,S_t,σ_t) \over \partial S_t \partial σ_t} ∆S_t ∆σ_t + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial σ_t^2} (∆σ_t)^2 \space \space (vii)\]
\[ Unexplained Var(P(t ; ζ_{t})) = {∆P(t ; ζ_{t})} -Explained Var(P(t ; ζ_{t})) \space \space (viii)\]
Ainsi, en théorie, si l’identification des facteurs de risque impactant le portefeuille est précise, on aura,
\[Unexplained Var(P(t ; ζ_{t}))≅0 \space \space (ix)\]
Dans le cas de produits complexes, dépendant d’un grand nombre de facteurs de risque non présents dans l’explication de la variation du portefeuille, on aura en revanche une différence matérielle entre les quantités \({∆P(t ; ζ_{t}) \over ∆t}\) et \(Explained Var(P(t ; ζ_{t}))\). On dit que le P&L du desk a de forts inexpliqués. C’est un problème récurrent sur certains desks et qui nécessite la mobilisation importante de ressources pour contrôler ce phénomène. Cela peut aller jusqu’à l’arrêt de l’activité par l’institution par incapacité de gérer les risques inhérents.
c. Alternatives
Une alternative de la représentation du P&L par les sensibilités est la méthode dite de réévaluation. On procède au recalcul intégral de la position sans décomposition. Cette approche ne génère normalement pas d’écarts inexpliqués mais ne permet plus la granularité offerte par l’approche précédente.
3. Calcul de sensibilités dans la Value-at-Risk
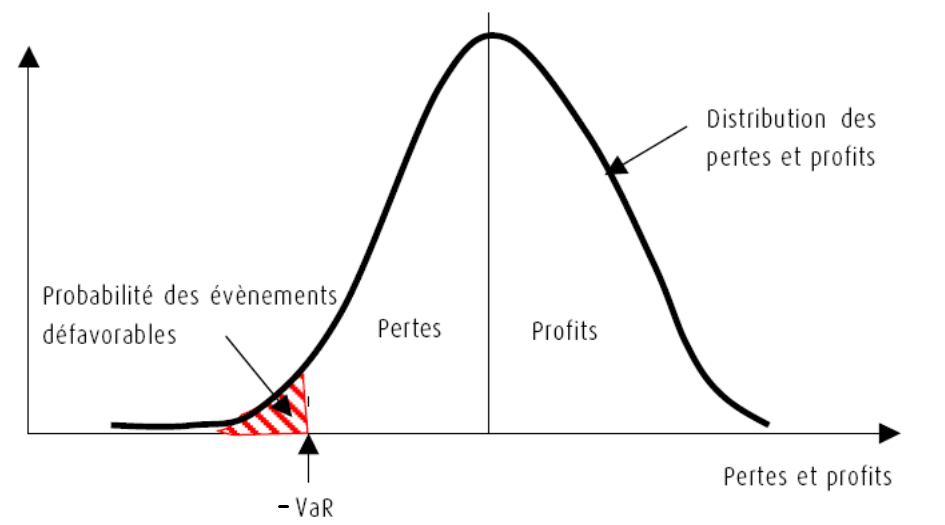
a. Qu’est-ce que la VaR?
Le P&L sert également pour le calcul de la valeur en risque quotidienne.
En effet, si on définit la perte sur une période comme étant \({L= -P\&L}\).
La valeur en risque, beaucoup plus connue sous le nom anglais Value-at-Risk ou VaR, est une mesure de la perte potentielle qui peut survenir à la suite de mouvements adverse des prix de marché et est définie à un seuil donnée par la relation :
\[Pr\{L ≤ -VaR(α)\} = α \space\]
Cela peut être traduit par : Combien l’établissement financier peut-il perdre avec une probabilité α pour l’horizon de temps h fixé ?
b. Peut-on intégrer les sensibilités dans la VaR ?
En remarquant que les dérivées partielles de l’équation (vii) capturent le passage du temps dit thêta (\({\partial F (t,S_t,σ_t) \over \partial t}\)), la variation du sous-jacent dit delta (\({\partial F (t,S_t,σ_t) \over \partial S_t}\)), la variation de la volatilité dit véga (\({\partial F (t,S_t,σ_t) \over \partial σ_t}\)), et les effets de second ordres dits gamma, vanna et volga (\({\partial^2 F (t,S_t,σ_t) \over \partial S_t^2}\),\({\partial^2 F (t,S_t,σ_t) \over \partial S_t \partial σ_t}\),\({\partial^2 F (t,S_t,σ_t) \over \partial σ_t^2}\)) et en introduisant des sensibilités adaptés aux rendements \(\tilde{δ}=δ*S_t\), \(\tilde{ϑ}=ϑ*σ_t\), \(\tilde{γ}=γ*S_t^2\), \(\tilde{vanna}=vanna*S_t σ_t\), \(\tilde{volga} = volga*σ_t^2\) on peut la réécrire comme suit :
\[ ∆P(t ; ζ_{t}) = θ ∆t + \tilde{δ} {∆S_t \over S_t} + \tilde{ϑ} {∆σ_t \over σ_t} \]
\[ + {1 \over 2}\tilde{γ} {(∆S_t)^2 \over S_t^2} + \tilde{vanna} {∆S_t ∆σ_t \over S_t σ_t} + {1 \over 2}\tilde{volga} {(∆σ_t)^2 \over σ_t^2} \space \space \space (xi)\]
Ou encore:
\[ ∆P(t ; ζ_{t}) = θ ∆t + \tilde{δ} R_s + \tilde{ϑ} R_σ \]
\[ + {1 \over 2}\tilde{γ} R_s^2 + \tilde{vanna} R_sR_σ + {1 \over 2}\tilde{volga}R_σ^2 \space \space (v) \space \space (xii)\]
Avec:
\[R_s = {∆S_t \over S_t} ; R_σ = {∆σ_t \over σ_t} \]
Sous forme matricielle on peut donc écrire:
\[∆P(t ; ζ_{t}) = {1 \over 2}* R^T \tilde{Γ}R + \tilde{π}^T R + θ*∆t \space \space (xii)\]
\[ \tilde{Γ} = \begin{bmatrix}\tilde{Γ_i,j}\end{bmatrix} = \begin{bmatrix} \tilde{γ} & \tilde{vanna} \\ \tilde{vanna} & \tilde{volga} \end{bmatrix} ; R = \begin{bmatrix} R_s \\ R_σ \end{bmatrix} ; \tilde{π} = \begin{bmatrix} \tilde{δ} \\ \tilde{ϑ} \end{bmatrix} \]
A ce stade, on peut aisément introduire les valeurs de R obtenues à partir d’une distribution fixe de structure de corrélation donnée par la matrice de variance covariance Σ.
Cela permet d’écrire les moments d’ordre 1 et 2 comme suit :
\[ μ_1(∆P(t ; ζ_{t}))={1 \over 2}*trace(\tilde{Γ} ̃Σ)+θ*∆t ; μ_2(∆P(t ; ζ_{t}))= {1 \over 2}*trace((\tilde{Γ}Σ)^2 )+ \tilde{π}^T Σ \tilde{π} \space \space (xiii)\]
Si on suppose à présent que la quantité \(∆P(t ; ζ_{t})\) suit une loi normale de moyenne \(μ_1(∆P(t ; ζ_{t}))\) et de variance \(μ_2 (∆P(t ; ζ_{t}))^2\) alors on obtient finalement :
\[ VaR_α = -(μ_1(∆P(t ; ζ_{t})) + μ_2 (∆P(t ; ζ_{t})) * z_{1-α} (0,1)) \space \space (xiv)\]
c. Avantages/inconvénients
Les avantages de cette approche sont les mêmes que la méthode du P&L par sensibilités, cela permet d’attribuer les variations de la mesure de risque aux changements des facteurs de risque. Aussi, étant donné que les sensibilités sont largement calculées et intégrées dans les systèmes de gestion des risques, cela ne demande le plus souvent que de simple ajustements.
Toutefois, et tout comme l’approche en sensibilités pour l’explication du P&L, une identification approximative des facteurs de risques impactant les transactions considérées et donc les mesures de risque sont sources d’écart dit inexpliqués pouvant devenir significatifs.
Aussi, dans le cadre de la VaR, on fait une hypothèse sur la distribution de P&L qui peut le cas échéant générer des écarts. Notamment si les rendements présente un caractère leptokurtique avec des queues de distributions épaisses. Les montants de VaR pourraient dans ce cas-là être sous-estimés.
4. Conclusion
L’utilisation des sensibilités dans l’explication du P&L est un outil puissant permettant d’attribuer les variations du P&L à des changements des facteurs de risque.
Cependant, l’approximation utilisée dans le calcul de l’explication de P&L n’est pas exacte et le processus d’identification des facteurs de risque est donc central. De fait, une bonne identification des facteurs de risque engendrera une explication du P&L quasi parfaite là où la sélection de facteurs de risque non significatifs peut entrainer une divergence entre le P&L et l’explication du P&L.
Lorsque le processus d’identification des facteurs de risque est maitrisée et donne des résultats satisfaisants, il est aisé d’étendre l’utilisation des sensibilités au calcul de la VaR, véritable mesure de perte potentielle d’une ligne de métier spécialisée sur un horizon donné.
Dans ce dernier cas, des hypothèses sur la distribution du P&L peuvent rendre les résultats imprécis, une vérification de ladite distribution via des tests statistiques pourrait diminuer les incertitudes.
En période de stress, où l'on observe des variations des facteurs de risque importantes,la régularité de la fonction de valorisation du portefeuille est souvent remise en cause et conduit aux limites d'applicabilité du théorème de Taylor.
Dans tous les cas, les méthodes de revalorisation intégrale sont une bonne alternative ne générant en théorie pas d’erreur liée à la sélection des facteurs de risque mais donnant un résultat unidimensionnel.
Warren Wamba
Consulting Engineer
Quantitative Advisory & Tactical Development