Is the use of sensitivities in explaining day-to-day P&L variations an effective method of measuring profitability and identifying market risk factors?
Last Updated on April 29,2020
1.What is P&L?
One of the main objectives of the Front-Office of an investment bank,subdivided into specialized business lines called "trading desks",is to reach the optimal compromise between risk and profitability.
The Profit&Loss Account(P&L for short)allows you to measure the profitability of trading desks over a given period(daily,monthly,annually,etc.).
Concretely,the P&L is made up of four principal components,the first is the change in the value of in-life,non-matured transactions of the desk over the calculation period,the second is the set of cash-flows of the desk over the period,the third constitutes specific value adjustments(reserves,specific adjustments-for instance,due to the valuation model used,fx related adjustments,etc.),the fourth constitutes all trading costs.
The sum of these four components constitutes the net P&L of the calculation period:
\[P\&L(t;t+h)=P(t+h;ζ_{t+h})-P(t;ζ_{t})+Add-On(t;t+h)\space \space(i)\]
With:
\[Add-On(t;t+h)=\sum_{i=t}^{t+h}CashFlows(i)+\sum_{j=t}^{t+h}Adjustments(j)+\sum_{k=t}^{t+h}Fees(k)\space \space(ii)\]
It is worth pointing out that \(P(t;ζ_{t})=MtM(desk-trans.,t)\)constitutes the market value of all the desk transactions at date t.
The calculation of this market value can be simple if the given transactions are vanilla instruments and if their price can be easily observed on the market.On the other hand,in the context of more complex products(exotic,highly path-dependent,structured,etc.)valuation requires the use of complex models that can generate uncertainties in the calculated P&L levels.
2.Use of sensitivities in P&L Explain
a.Principle
The P&L is used as described above by many financial institutions as a measure of the economic profitability of market activities over a given period.
Between two periods,observing a change in P&L levels may lead to determining the risk factors that produced this change and optimizing the composition of the portfolio accordingly.
The idea is to arrive at the optimal trade-off between exposure/risk factors and the income of the activity.That is risk management.
An assumption often made is that the function \(P(t;ζ_{t})\)and,therefore,the P&L is a \(C^{n+1}\)function on \(I=R*R^p \)with value in \(R\)and therefore that's Taylor's theorem is applicable.
For instance,within the framework of market-options,one can write:
\(P(t;ζ_{t})=F(t,S_t,σ_t),\)with \(ζ_{t}=\{S_t,σ_t\}\space \space(iii)\)
With variables:
- \(S_t\):Price of the underlying asset
- \(σ_t\):Volatility of the underlying asset
The application of Taylor's theorem, therefore, leads us to the following expression:
\[ {∆P(t ; ζ_{t})} = { ∆F (t,S_t,σ_t)} \space \space (iv)\]
\[ {∆P(t ; ζ_{t})} = {\partial F (t,S_t,σ_t) \over \partial t} ∆t + {\partial F (t,S_t,σ_t) \over \partial S_t} ∆S_t + {\partial F (t,S_t,σ_t) \over \partial σ_t} ∆σ_t \]
\[ + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial S_t^2} (∆S_t)^2 + {\partial^2 F (t,S_t,σ_t) \over \partial S_t \partial σ_t} ∆S_t ∆σ_t + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial σ_t^2} (∆σ_t)^2 \space \space (v)\]
This rewriting of the change in the portfolio value between two times in terms of partial derivatives of the portfolio's market valuation function is called the P&L attribution to first and second-order market sensitivities.
b.Advantages/disadvantages
The strength in expressing the change in the value of the trading portfolio as a function of given changes in its valuation parameters(i.e.,risk factors)is in being able to attribute the P&L level to a change in the yield curve,the volatility,the value of the underlying,etc.
The P&L and the P&L explain above are,therefore,central elements of the risk management process,which are measured and analyzed daily in investment banks.
Indeed,it is possible to immunize the portfolio and,therefore,the P&L against variations in a given risk factor(e.g.,level of volatility,level of the underlying,etc.).
However,it should be recalled that Taylor's development is not equality and, in fact, there is a so-called integral remainder by application of the fundamental theorem of analysis:
\[ {∆P(t ; ζ_{t})}= Explained Var(P(t ; ζ_{t}))+Unexplained Var(P(t ; ζ_{t})) \space \space (vi)\]
With:
\[ Explained Var(P(t ; ζ_{t})) = {\partial F (t,S_t,σ_t) \over \partial t} ∆t + {\partial F (t,S_t,σ_t) \over \partial S_t} ∆S_t + {\partial F (t,S_t,σ_t) \over \partial σ_t} ∆σ_t \]
\[ + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial S_t^2} (∆S_t)^2 + {\partial^2 F (t,S_t,σ_t) \over \partial S_t \partial σ_t} ∆S_t ∆σ_t + {1 \over 2}{\partial^2 F (t,S_t,σ_t) \over \partial σ_t^2} (∆σ_t)^2 \space \space (vii)\]
\[ Unexplained Var(P(t ; ζ_{t})) = {∆P(t ; ζ_{t})} -Explained Var(P(t ; ζ_{t})) \space \space (viii)\]
So, in theory, if the identification of the risk factors impacting the portfolio is precise, we will have,
\[Unexplained Var(P(t ; ζ_{t}))≅0 \space \space (ix)\]
In the case of complex products, with dependency on a large number of risk factors not incorporated in the P&L explain, there will be a material difference between the quantities \({∆P(t ; ζ_{t}) \over ∆t}\) and \(Explained Var(P(t ; ζ_{t}))\). It is said that the desk's P&L has material unexplained.This is a recurring challenge on some desks and requires the mobilization of many resources.That can lead to the extinction of the trading activity by the institution for failure to manage the inherent risks.
c.Alternatives
An alternative to the P&L attribution to sensitivities is the so-called revaluation method.One proceeds to the integral recalculation of the positions without decomposition.In theory,this approach does not generate unexplained discrepancies but no longer allows the granularity of the previous method.
3.Calculation of sensitivities in Value-at-Risk
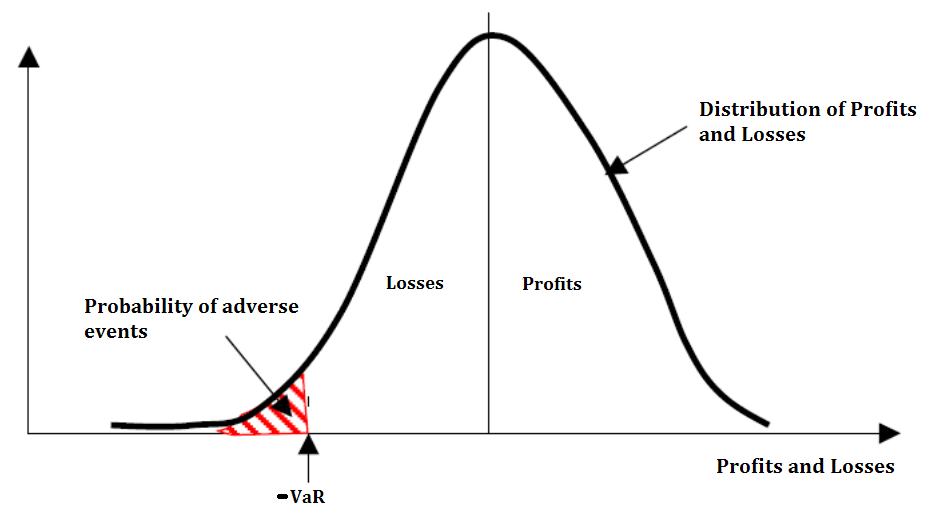
a.What is VaR?
The P&L is also used to calculate the daily Value-at-Risk.
Indeed,if we define the loss over a period as \({L=-P\&L}\).
The Value-at-Risk,or VaR for short,is a measure of the potential loss that can occur following adverse movements in market prices and is defined at a confidence level for a predefined time horizon.It is given by the relationship:
\[Pr\{L ≤-VaR(α)\}=α \space\]
This can be translated as:How much can the financial institution lose with a probability α for the fixed time horizon h?
b.Can we integrate sensitivities in VaR?
By noting that the partial derivatives of the equation(vii)capture the passage of time named theta(\({\partial F(t,S_t,σ_t)\over \partial t}\)),the variation of the underlying named delta(\({\partial F(t,S_t,σ_t)\over \partial S_t}\)),the variation of the volatility named vega(\({\partial F(t,S_t,σ_t)\over \partial σ_t}\)),and the second-order effects named gamma,vanna,and volga,respectively,(\({\partial^2 F(t,S_t,σ_t)\over \partial S_t^2}\),\({\partial^2 F(t,S_t,σ_t)\over \partial S_t \partial σ_t}\),\({\partial^2 F(t,S_t,σ_t)\over \partial σ_t^2}\))and by introducing sensitivities adapted to returns \(\tilde{δ}=δ*S_t\),\(\tilde{ϑ}=ϑ*σ_t\),\(\tilde{γ}=γ*S_t^2\),\(\tilde{vanna}=vanna*S_t σ_t\),\(\tilde{volga}=volga*σ_t^2\),we can rewrite it as follows:
\[∆P(t;ζ_{t})=θ ∆t+\tilde{δ}{∆S_t \over S_t}+\tilde{ϑ}{∆σ_t \over σ_t}\]
\[+{1 \over 2}\tilde{γ}{(∆S_t)^2 \over S_t^2}+\tilde{vanna}{∆S_t ∆σ_t \over S_t σ_t}+{1 \over 2}\tilde{volga}{(∆σ_t)^2 \over σ_t^2}\space \space \space(xi)\]
Or:
\[∆P(t;ζ_{t})=θ ∆t+\tilde{δ}R_s+\tilde{ϑ}R_σ \]
\[+{1 \over 2}\tilde{γ}R_s^2+\tilde{vanna}R_sR_σ+{1 \over 2}\tilde{volga}R_σ^2 \space \space(v)\space \space(xii)\]
With:
\[R_s={∆S_t \over S_t};R_σ={∆σ_t \over σ_t}\]
Therefore,we can write in matrix form:
\[∆P(t;ζ_{t})={1 \over 2}*R^T \tilde{Γ}R+\tilde{π}^T R+θ*∆t \space \space(xii)\]
\[\tilde{Γ}=\begin{bmatrix}\tilde{Γ_i,j}\end{bmatrix}=\begin{bmatrix}\tilde{γ}&\tilde{vanna}\\ \tilde{vanna}&\tilde{volga}\end{bmatrix};R=\begin{bmatrix}R_s \\ R_σ \end{bmatrix};\tilde{π}=\begin{bmatrix}\tilde{δ}\\ \tilde{ϑ}\end{bmatrix}\]
At this stage,we can easily introduce the values of R obtained from a fixed distribution of correlation structure given by the variance-covariance matrix Σ.
This makes it possible to write the first and second-order moments as follows:
\[μ_1(∆P(t;ζ_{t}))={1 \over 2}*trace(\tilde{Γ}̃Σ)+θ*∆t;μ_2(∆P(t;ζ_{t}))={1 \over 2}*trace((\tilde{Γ}Σ)^2)+\tilde{π}^T Σ \tilde{π}\space \space(xiii)\]
If we now assume that the quantity \(∆P(t;ζ_{t})\)follows a normal law of mean \(μ_1(∆P(t;ζ_{t}))\)and variance \(μ_2(∆P(t;ζ_{t}))^2\),we finally get:
\[VaR_α=-(μ_1(∆P(t;ζ_{t}))+μ_2(∆P(t;ζ_{t}))*z_{1-α}(0,1))\space \space(xiv)\]
c.Advantages/disadvantages
The advantages of this approach are the same as those of the P&L explain method;it allows for attribution of the variations of the risk measure to changes in risk factors.Also,because sensitivities are largely calculated and integrated into risk management systems,this usually requires only marginal adjustments.
However,and just like the P&L explain method,flaws in the process of identification of the key risk factors impacting the considered transactions.Therefore,the calculated risk measures are sources of so-called unexplained discrepancies that can become material.
Also,within the VaR framework,we make an assumption about the P&L distribution which can generate differences,especially if the returns exhibit a leptokurtic character with fat tails.In this scenario,the VaR levels could be underestimated.
4.Conclusion
The use of sensitivities in P&L explain is a powerful tool for attributing P&L variations to changes in risk factors.
However,the P&L explain is an approximation and,as a result,is not exact.Therefore,the process of identifying key risk factors is central.In fact,proper identification of key risk factors will lead to satisfactory P&L explain.Yet,the selection of non-material risk factors and the non-consideration of risk-factor interdependencies can lead to a divergence between P&L and P&L explain.
When the process of identifying key risk factors is well-managed and produces satisfactory results,it is easy to extend the use of sensitivities to the VaR calculation,a real measure of the potential loss of a specialized business line over a given horizon.
In the latter case,hypotheses on the P&L distribution can make the results inaccurate.Verification of assumed distribution via statistical tests could reduce uncertainties.
In a period of turmoil,when huge variations in risk factors can be observed,the regularity of the portfolio's market valuation function is often in question and leads to limits in the applicability of Taylor's theorem.
In all cases,the integral revaluation methods are a good alternative that,in theory,does not generate any error linked to the selection of risk factors but gives a one-dimensional result.
Warren Wamba
Consulting Engineer
Quantitative Advisory&Tactical Development